For n>2, we will show a winning arrangement and a winning strategy for the second player. This strategy revolves around the concept of "traps". A trap is an odd-sized connected set of high-valued cells surrounded by low-valued cells in the set of all its immediate neighbors, which must also be of odd size.
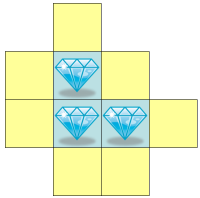
Here is an example of such a trap, with diamonds signifying high values and empty cells signifying low values.

Notably, the total number of cells composing a trap is even.
Suppose that we tile the board into connected sets, each of even size. A feasible strategy of the second player will be in this case "Consider only values that are of the same set as the first player took from in her latest turn. Of these, remove the highest possible." If one of the sets is a trap and the first player steps into it (removes a first value from it), this cell will necessarily contain a low value. The second player, following her strategy, will take a high value. Ultimately, the trap will be emptied with the second player taking at least one more high value than the first.
We will need an arrangement with at least three traps. The reason for this is that the first player can choose where to begin in the first move, and she can avoid one trap by beginning in one of its high-valued positions. As the first player can choose to do this with the trap for which the prize is highest, we will need at least two additional traps to counter-balance this.
We will not use the kidney-bean shaped trap described above, because it is too large for our purposes. Instead, we will use the smallest possible trap:
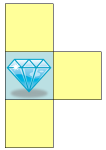
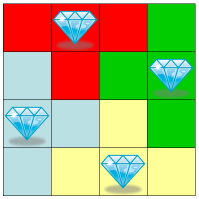
This is a trap, provided that the middle piece of the trap is an edge piece of the board, and therefore has exactly three neighbors. On a 4x4 board, four such traps can be placed in the following arrangement:
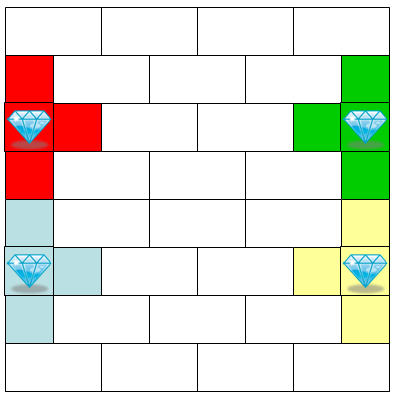
On any larger board, we'll place four such traps along with domino tiles to complete the rest of the board in a formation such as the one demonstrated below for 8x8:
We will place in each trap the values a, a+1 and a+2 for the low-valued cells and b for the high-valued cell, for some such a and b. This configuration insures that the sum of values taken by the second player is at least b-a-3 larger than that of the first player, for cells taken from the trap, provided that the first player doesn't choose to begin the game in the high-valued cell. If she does, the sum of the cell values taken from the trap by the first player will be no more than b-a-1 greater than that of the second player.
We will place in each domino piece two consecutive numbers, insuring that the advantage gained by the first player on each such tile is at most 1.
Suppose the values used in the four traps are:
The best strategy of the first player is to begin the game inside the first trap. This will give her n2-5 for that trap. She will also get one point for each of the n2/2-8 domino tiles. However, she will lose n2-9 for the second trap, n2-11 for the third and n2-13 for the fourth, resulting in a total balance of 1.5n2-20, which, for n≥4 is in favor of the second player.
The nice thing about this arrangement is that both players have a clear best strategy: the first player starts with the high-valued cell of the trap with the highest b-a value, then continues by always picking the highest possible value, excluding values within the traps. Once all the rest of the board is empty, the first player goes into the traps in such a way that the a+2 and a+1 values will be hers.
The strategy for the second player (given the strategy of the first player and the arrangement of the board) is as follows: if the first player took a value from a trap, take the highest possible value within that trap. If not, take the highest possible value from outside any trap.
Now, the question is merely what the values of the traps are, to determine who wins. Here is a possible arrangement (the notation of which will be explained immediately aftrwards):
ZZZAAABBBCCCDDD .... XXXYYYYX .... DCBAZ
The notation used here is as follows: the first letter signifies the identity of the trap to which the value n2-4k+1 belongs. The next, signifies the identity of the trap to which the value n2-4k+2 belongs, and so on, with the last letter signifying the identity of the trap to which the value n2 belongs. The first three values and the last value belong to the trap denoted as "Z". This means that this trap has n2-4k+1 as its a value and n2 as its b value, making it the highest valued trap.
In the arrangment, the second player can reach a tie on the "Y" trap, gain 4 points on the "X" trap, and so on, with the "A" trap allowing the second player to gain 4k-8 points on it. In both cases, the "Z" trap can, potentially, be used by the second player to gain 4k-4 points, but, in fact, the first player will start within it, taking the n2 value first, so it will actually give the first player an advantage of 4k-2.
Consider the final total balance. The first player can gain (n2-4k)/2 points for all values outside traps plus an additional 4k-2 on the "Z" trap, giving her a total advantage of n2/2+2k-2. However, the remaining traps set the balance back by 2(k-2)(k-1) to a total of n2/2-2k2+8k-6 or n2/2-2(k-2)2+2.
Choosing k to be n/2+2 makes the first player win by exactly two points.
Now, we will tweak this arrangement slightly, by replacing the high values of the "Z" trap and the "A" trap to form this new arrangement:
ZZZAAABBBCCCDDD .... XXXYYYYX .... DCBZA
The "Z" trap, though its b value has been lowered by 1, is still the most valuable trap, so the first player will start from it. On the other hand, the "A" trap's b value has been raised by 1. This sets the first player's total balance back by 2, causing a tie exactly.
The only remaining question is whether k=n/2+2 can be afforded in every case where n>2. In fact, one can arrange along the sides of an n by n board a number of traps that is equal to 4n/3 up to a constant. By simple trial and error, one can find that a 4x4 board accomodates four traps, a 6x6 - five and an 8x8 - eight. (One would have been able to fit six on a 6x6 board, if we didn't require for the remaining pieces to be connected.) For any larger shape, note that one can create an arrangement for an (n+6)x(n+6) board given an n by n board by simply keeping each trap at a constant position relative to its nearest corner and adding two traps to each side in the positions that become freed. This adds 8 traps when raising n by six, which is much more than the required three.