Let us assign each invitee a different numerical value in modulo 2n (not assigning any number to Arthur himself). The operation "+" used in the description below will denote modulo 2n addition.
Let us first solve the following, simpler problem: we would like a scheme for a party that lasts 2n nights, during which no person "A" will be seated to the right of the same person "B", twice. (This is different from the original question in that the original question was bidirectional.)
A solution for this riddle is as follows. Let T be a permutation over the numbers 0 through 2n-1 and let j designate the date from 0 (the first night of the party) to 2n-1 (the last). We will seat to Arthur's left guest T0+j, followed by guest T1+j, etc., until guest T2n-1+j who will sit immediately to Arthur's right. T0 will be set, arbitrarily, to 0. The question is, for which permutation T does this constitute a valid arrangement?
Let us suppose on the contrary that the arrangement is invalid, then there are two nights, j and k, with j≠k, such that for some x and y, Tx+j=Ty+k (=person "A") while Tx+1+j=Ty+1+k (=person "B").
Subtracting the two equations, we have Tx+1-Tx = Ty+1-Ty. A valid solution is one in which this implies x=y. Let us denote for all i between 1 and 2n-1 Si=Ti-Ti-1. The derivation so far implies that the solution is valid if and only if S is a permutation over the numbers between 1 and 2n-1.
Constant readers of UyHiP will recognize that already in the first part of the previous riddle (May 2008) we have shown that a solution exists for any n.
Returning to the full, bidirectional version of the riddle, let us create a solution to the unidirectional, simpler riddle in which during night j the guests are arranged in the reverse order to their arrangement during night 2n-j (If "A" was to the right of "B" on night j, she will be to his left on night 2n-j).
Such a solution can easily be made into a bidirectional solution by taking the first n nights only. Referring again to the May 2008 riddle, the existence of a solution is guaranteed by the second part of that riddle.
Q.E.D.
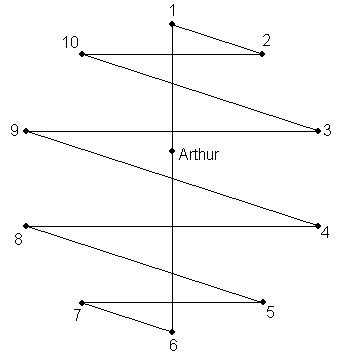
Bojan Bašić sends the following graphical description of the solution (illustrated here for n=5):

The arrangements for the various nights can be reached by rotating the shape in multiples of 36 degrees.
As a side-note, readers seeking a way to intuit the solution should consider what happens when 2n+1 is a prime, p. Placing guest ij (mod p) in table position i at night j (j being counted starting from 1) is clearly an immediate solution, because any two adjacent guests on night j will be numbered j apart. The solution to the riddle stems from a different method of proving that this is a valid solution, namely by showing that the ratio of the numbers assigned to any two adjacently-seated guests is unique in the arrangement of any particular night. This validity criterion has the advantage that it requires the use of only one numerical operation (multiplication), and can therefore be applied to groups of any size, not necessarily prime. The solution to this month's riddle can be viewed as the discrete log of this arrangement (with Arthur playing the part of "log 0").