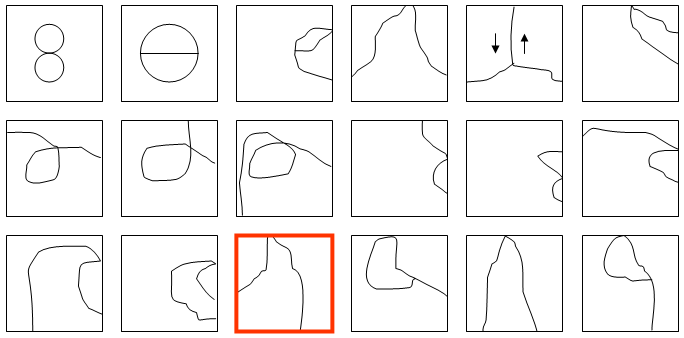

The interesting thing about all these alternatives is that there is only a finite number of them, and the number is small enough for one to analyze each variation separately. Within each topological alternative, the optimal arrangement is fairly easy to discover once one figures out several basic rules that can be found by use of calculus of variations. Such rules include, as examples:
Of all the topologically distinct alternatives, the one that ultimately yields the shortest path is the one indicated in the figure above by a red frame. By applying the rules mentioned above, we see that the optimal solution should be constructed of two circle segments, as in the figure below.
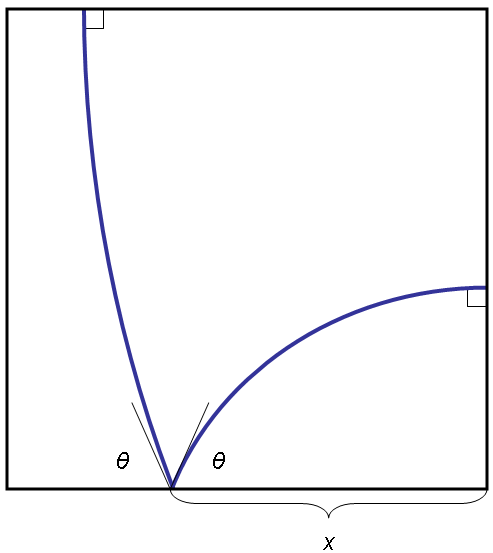
By solving the equations to insure that the square is, indeed, cut to three equal-area shapes, θ turns out to equal approximately 88.838359 degrees, x turns out to equal approximately 0.6599081, and the total length of the cut equals approximately 2.02348085728, or 2.023481 when truncated to six decimal places.