Using your Head is Permitted

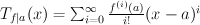
where f⁽ⁱ⁾(a) is the i'th derivative of f at a.

In many cases, when f is a smooth function, a Taylor series T_f|a(x) is used as a convenient approximation to f(x).

A smooth function, for our purposes, more properly termed a C^∞ function, is a function that is continuous, infinitely many times differentiable, and that all of its derivatives are also continuous, and all this in the entire domain in which it is defined.

However, even given all these requirements, it is still not guaranteed that a Taylor series converges at any particular point, x, or, if it does, that T_f|a(x)=f(x). In fact, let us define the set Χ_f|a to be the set of all points, x, in which T_f|a(x) exists and equals f(x).

This month's question:

f is a smooth function defined on ℜ⁺ (the positive real numbers). It satisfies the property that for all d ∈ ℜ⁺ there exist a and u ∈ ℜ⁺ such that Χ_f|a is the open segment (u,u+d).

Your task: find one such f (preferably a simple one).

Readers are asked to refrain from looking up any texts that give examples of Taylor series in solving this riddle. Most basic introductions to Taylor series fall into this category.

Correction: Though the riddle, as written above, has solutions, and one such solution is documented on the answer page, the original riddle was meant to be much simpler and the original solution was meant to be much more elegant. In order to allow for a simple, elegant solution, one should allow u to be nonnegative, and not only strictly positive. The restriction that u should be positive was unintended, and was put in the original wording in error.

List of solvers: