Using your Head is Permitted

UPDATE (5 September): Based on the answers I've been getting, it seems I have not done too good a job at explaining the format I'm asking for, from the solution. Consider, therefore, the image below.

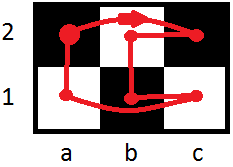
This picture depicts a 3-by-2 chessboard, and on it (in red) the path of a rook. The rook begins at a2, moves to c2, then left to b2, down to b1, right to c1, left again to a1, and then up to a2 to complete its tour. This will be depicted in the solution as follows:

000201
050304

The solution contains here 2 lines, each with 3 pairs of digits. This is because the board is 3-by-2. Each pair of digits corresponds to a square on the board. The value associated with each pair of digits, ranging from 00 to 05, gives the information of the move number on which the rook alights at that particular square: it begins at the 00 square, moves on to the 01 square, from there to the 02 square, etc..

I hope this clarifies the issue.

This month's question comes from Yaron Gvili. More credits will be given on the solution page.

Consider a rook traveling in legal rook moves across a standard 8x8 chessboard. We are interested in closed rook tours. That is, we are interested in a sequence of 64 consecutive moves made by the rook that visits every square on the board exactly once, and returns ultimately to the original position.

The object this month is to find a path which can be taken by the rook that maximizes the total distance traveled. (For example, a move from "e1" to "e3" requires two units of distance to be traveled.)

Uncharacteristically for Using your Head is Permitted, this month no proof of optimality is required. (However, if you send in a proof, you will get an asterisk next to your name.)

To be considered a solver, please send in your proposed rook tour in the following format. Send in 8 lines of text, each with 8 consecutive pairs of digits. Each pair denotes a position on the board, and the value of the two-digit number should be a value between 0 and 63, denoting at which move the rook traveled to this board position. For example, if the question was asked for a 2x2 board, one solution would have been

0001
0302

a2	b2
a1	b1

List of solvers: